Per i ragazzi della III A
Nel link seguente trovate gli argomenti di Dinamica svolti a lezione. Buono studio.
Appunti
lunedì 19 dicembre 2016
Algebra (monomi e polinomi + esercizi)
Per i ragazzi della III F
Nel link seguente trovate gli argomenti spiegati a lezione. Buono studio!
Appunti
Nel link seguente trovate gli argomenti spiegati a lezione. Buono studio!
Appunti
mercoledì 23 novembre 2016
Aceto e Bicarbonato
Per i ragazzi della II F
In classe abbiamo realizzato una reazione chimica facendo reagire aceto e bicarbonato di sodio.
2. Abbiamo messo del bicarbonato nel palloncino.
3. Abbiamo inserito il collo della bottiglia nella bocca del palloncino.
4. Abbiamo lasciato cadere il bicarbonato dentro la bottiglia, contenente l’aceto.
Osservazioni
Abbiamo notato che dopo aver versato il bicarbonato (che era nel palloncino) dentro l’ aceto, le sostanze hanno iniziato a fare delle bollicine e della schiuma; a questo punto il palloncino ha iniziato a gonfiarsi.
Interpretazione chimica
Tra aceto e bicarbonato è avvenuta una reazione chimica; ciò significa che le due sostanze non si sono semplicemente mescolate, ma che le molecole dell’una e le molecole dell’altra si sono “smontate” e gli atomi che le formavano si sono riuniti a formare nuove molecole, di sostanze diverse.
L’acido acetico (aceto) e il bicarbonato di sodio, ossia le sostanze presenti all’inizio, sono detti reagenti; le sostanze presenti dopo che è avvenuta la reazione chimica sono dette prodotti della reazione.
In questo caso i prodotti sono tre:
La reazione a cui abbiamo assistito può essere così schematizzata:
CH3COOH + NaHCO3 → CH3COONa + H2O + CO2
Come si vede, a sinistra della freccia sono indicati i reagenti, a destra i prodotti. Le molecole presenti all’inizio e alla fine sono completamente diverse. Nessun atomo però è andato perduto e nessun atomo è comparso dal nulla, come schematizzato nella seguente tabella:
Quindi il numero totale di atomi nei reagenti e nei prodotti è lo stesso.
Questo risultato è una conseguenza della legge di Lavoisier che afferma: "in una reazione chimica la massa dei reagenti è uguale a quella dei prodotti".
In classe abbiamo realizzato una reazione chimica facendo reagire aceto e bicarbonato di sodio.
Materiali e strumenti usati
- Un palloncino
- Una bottiglia trasparente da un litro
- Due dita d’aceto
- Bicarbonato
Esecuzione dell’esperimento
1. Nella bottiglia abbiamo versato due dita d’aceto, poi abbiamo preso il palloncino ed il bicarbonato.2. Abbiamo messo del bicarbonato nel palloncino.
3. Abbiamo inserito il collo della bottiglia nella bocca del palloncino.
4. Abbiamo lasciato cadere il bicarbonato dentro la bottiglia, contenente l’aceto.
Osservazioni
Abbiamo notato che dopo aver versato il bicarbonato (che era nel palloncino) dentro l’ aceto, le sostanze hanno iniziato a fare delle bollicine e della schiuma; a questo punto il palloncino ha iniziato a gonfiarsi.
Interpretazione chimica
Tra aceto e bicarbonato è avvenuta una reazione chimica; ciò significa che le due sostanze non si sono semplicemente mescolate, ma che le molecole dell’una e le molecole dell’altra si sono “smontate” e gli atomi che le formavano si sono riuniti a formare nuove molecole, di sostanze diverse.
L’acido acetico (aceto) e il bicarbonato di sodio, ossia le sostanze presenti all’inizio, sono detti reagenti; le sostanze presenti dopo che è avvenuta la reazione chimica sono dette prodotti della reazione.
In questo caso i prodotti sono tre:
- l’anidride carbonica (detta anche biossido di carbonio), che è il gas che ha fatto gonfiare il palloncino;
- l’acetato di sodio, che è il sale che precipita sul fondo;
- l’acqua, che rimane nella bottiglia insieme all’aceto che eventualmente non ha reagito, e che essendo trasparente schiarisce il colore del liquido presente nella bottiglia.
La reazione a cui abbiamo assistito può essere così schematizzata:
CH3COOH + NaHCO3 → CH3COONa + H2O + CO2
| CH3COOH | NaHCO3 | CH3COONa | H2O | CO2 |
| Acido acetico | Bicarbonato di sodio | Acetato di sodio | Acqua | Anidride carbonica |
Come si vede, a sinistra della freccia sono indicati i reagenti, a destra i prodotti. Le molecole presenti all’inizio e alla fine sono completamente diverse. Nessun atomo però è andato perduto e nessun atomo è comparso dal nulla, come schematizzato nella seguente tabella:
| Atomi di Idrogeno (H) | Atomi di Ossigeno (O) | Atomi di Carbonio (C) | Atomi di Sodio (Na) | |
| Reagenti | 5 | 5 | 3 | 1 |
| Prodotti | 5 | 5 | 3 | 1 |
Quindi il numero totale di atomi nei reagenti e nei prodotti è lo stesso.
Questo risultato è una conseguenza della legge di Lavoisier che afferma: "in una reazione chimica la massa dei reagenti è uguale a quella dei prodotti".
domenica 20 novembre 2016
Proprietà tipiche dei liquidi
Per i ragazzi della I F
1. Tensione superficiale
Se lasci cadere
delicatamente una goccia d'acqua su una superficie liscia non
assorbente, ad esempio il tuo banco, essa forma una piccola massa
rotonda di aspetto compatto ciò accade a causa delle forze di
coesione esistenti tra le molecole. Grazie a
tali forze, sulla superficie dell'acqua si forma una specie di
pellicola elastica tesa: questo fenomeno
è detto TENSIONE SUPERFICIALE.
La tensione superficiale
è ciò che permette la formazione di gocce di rugiada sulle foglie o
a insetti come l'idrometra di camminare sull'acqua.
Per
capire meglio in cosa consiste la tensione superficiale e come agisce
il sapone su di essa, abbiamo eseguito un semplice esperimento in
classe durante le ore di scienze
2. Forze di adesione e
capillarità
Due liquidi diversi, per
esempio l'acqua e il mercurio, si comportano in modo diverso se
versati in un recipiente: l'acqua bagna le pareti del recipuente e la
sua superficie si incurva llegermente verso il basso (menisco
convesso), il mercurio non bagna le pareti e la sua superficie si
incurva verso l'alto (menisco concavo).
Questo fenomeno è
possibile perché oltre alle forze di coesione tra molecole della
stessa sostanza, esistono forze attrattive, dette forze di
adesione, che si sviluppano tra le sostanze e il recipiente che
le contiene.
Tra l'acqua e il vetro
del recipiente le forze di adesione prevalgono su quelle di coesione,
quindi l'acqua aderisce al vetro e tende a salire lungo le pareti;
tra il mercurio e il vetro le forze di coesione sono quasi
inesistenti, minori rispetto a quelle di coesione, quindi il mercurio
si “allontana” dalle pareti.
Nella figura seguente sono disegnate le forze di coesione e adesione nel caso dell'acqua.
Se immergi un tubicino,
cioè di sezione inferiore ai 2 mm, in un recipiente d'acqua puoi
osservare che 'acqua sale velocemente all'interno del tubicino
raggiungendo un livello più alto di quello che ha nel recipiente.
Se fai la stessa prova
con il mercurio, puoi osservare che il mercurio nel capillare
raggiunge un livello più basso di quello che ha nel recipiente.
Anche il fenomeno della
capillarità è legato
all''esistenza delle forze di adesione. Se appoggi l'estremità di
una striscia di carta assorbente sulla superficie dell'acqua colorata
contenuta in un recipiente, in breve tempo tutta la striscia risuterà
imbevuta.
La
carta ha la proprietà di attirare rapidamente le particelle di
acqua, vincendo anche la forza di gravità. Questo accade perché la carta è costituita da fibre sottilissime lungo le quali l’acqua
sale per capillarità.
In
natura i fenomeno della capillarità permette all'acqua di salire
dalle radici fino ai rami più alti delle piante, assicurandone così
il nutrimento.
giovedì 3 novembre 2016
Problemi sulle figure simili
Similitudine
- Due rettangoli hanno le basi rispettivamente di 40 cm e 80 cm . In quale rapporto devono essere le loro altezze perché siano simili?
- Un triangolo ha i lati che misurano 12 cm, 9 cm e 18 cm. Calcola il perimetro di un triangolo simile che ha il lato corrispondente al primo lato del primo triangolo pari a 18 cm.[58,5]
- In un triangolo i lati misurano rispettivamente 81 cm, 45 cm e 72 cm. Un secondo triangolo simile al primo ha il perimetro di 22 cm. Determina la misura della lunghezza dei lati del secondo triangolo.
- Due rettangoli hanno il perimetro rispettivamente di 60 cm e 72 cm . Si sa che sono simili: qual è il rapporto di similitudine? Qual è il rapporto fra le aree?
mercoledì 2 novembre 2016
domenica 16 ottobre 2016
giovedì 13 ottobre 2016
Problemi di Cinematica
Ciao a tutti,
nel link seguente https://drive.google.com/drive/folders/0B6sPZGuDSFpSTGRSTGU2OVdaS1k trovate dei problemi di cinematica su cui esercitarvi per la verifica. Nota: Il moto circolare non va fatto.
Se avete problemi o dubbi, commentate il post!
nel link seguente https://drive.google.com/drive/folders/0B6sPZGuDSFpSTGRSTGU2OVdaS1k trovate dei problemi di cinematica su cui esercitarvi per la verifica. Nota: Il moto circolare non va fatto.
Se avete problemi o dubbi, commentate il post!
lunedì 26 settembre 2016
Il dilemma del prigioniero
Il dilemma del prigioniero
...e
l'assioma di razionalità
Confessare o non confessare?
Aldo e Baldo sono sospettati di aver commesso una rapina insieme.La polizia li arresta entrambi e li chiude in due celle separate, in modo che non possano comunicare.
Il giudice non ha prove sufficienti per poterli condannare, perciò offre a ciascuno di loro un accordo. Le regole dell'accordo sono le seguenti:
- se solo uno dei due confessa, implicando anche l'altro, chi ha confessato evita la pena mentre l'altro viene condannato a 7 anni di carcere;
- se entrambi confessano, entrambi sono condannati a 5 anni.
- se nessuno dei due confessa, entrambi sono condannati a 1 anno.
credit:
Poojadfp's Blog
L'assioma di razionalità
Per risolvere il dilemma è utile conoscere l'assioma di razionalità che è alla base della teoria dei giochi.L’assioma di razionalità afferma che: nessun giocatore sceglierebbe mai una strategia se ne ha a disposizione un’altra che gli permette di ottenere risultati migliori, qualunque sia il comportamento dell’avversario.
Ma... che cosa significa "ottenere risultati migliori"?
Significa che il giocatore è in grado di ordinare le sue preferenze.
”Ordinare le sue preferenze” vuol dire che, dati due
risultati x e y (esempio: x =disporre di 4000 euro e y = avere un biglietto
aereo per i Caraibi), il giocatore è sempre in grado di dire se per lui:
a) x è meglio di y (x > y),
b) y è meglio di x (y > x),
c) o se sono allo stesso livello (x = y).
(tratto da Alessandro Agnetis, Introduzione alla Teoria dei Giochi)
a) x è meglio di y (x > y),
b) y è meglio di x (y > x),
c) o se sono allo stesso livello (x = y).
(tratto da Alessandro Agnetis, Introduzione alla Teoria dei Giochi)
Spesso si assume che un decisore, oltre che razionale, sia
anche intelligente. Questo termine indica semplicemente la
capacità logica di saper riconoscere le azioni necessarie per massimizzare la
propria utilità, ossia per agire in modo razionale.
(tratto da Alessandro Agnetis, Introduzione alla Teoria dei Giochi)
(tratto da Alessandro Agnetis, Introduzione alla Teoria dei Giochi)
Giochi cooperativi/non cooperativi
Il dilemma del prigioniero è un esempio di gioco non cooperativo.Che cosa significa?
Giochi cooperativi (J. Von Neumann): si
studia il formarsi di coalizioni con accordi sottoscritti e vincolanti che
possono essere di vantaggio ai singoli componenti.
Giochi non cooperativi (Nash): si studiano i meccanismi delle decisioni dei singoli sulla base di ragionamenti individuali in assenza di alleanze vincolanti. Non c’è spazio per la cooperazione perchè gli interessi sono contrastanti anche se ciò non significa necessariamente che una delle parti deve perdere per forza.
(tratto da Anna Grazia Quaranta, Teoria dei Giochi ed Applicazioni in Economia)
Giochi non cooperativi (Nash): si studiano i meccanismi delle decisioni dei singoli sulla base di ragionamenti individuali in assenza di alleanze vincolanti. Non c’è spazio per la cooperazione perchè gli interessi sono contrastanti anche se ciò non significa necessariamente che una delle parti deve perdere per forza.
(tratto da Anna Grazia Quaranta, Teoria dei Giochi ed Applicazioni in Economia)
venerdì 23 settembre 2016
Esercizi sugli Insiemi
ESERCIZI SULLE PROPRIETÀ DEGLI INSIEMI
Ricorda che un insieme è un raggruppamento di elementi definibili con precisione.
1) Indica quali dei seguenti raggruppamenti rappresentano un insieme in senso matematico:
a. l'insieme delle vocali presenti nel tuo cognome;
b. l'insieme dei numeri naturali minori di 5;
c. le più belle città d'Italia;
d. gli stati d'Europa;
e. i compagni più simpatici della tua classe.
ESERCIZI SULLA RAPPRESENTAZIONE DEGLI INSIEMI
Ricorda che un insieme si può rappresentare in tre modi:
A) con i diagrammi di Eulero-Venn, che sono formati da un ovale all'interno del quale si segnano con un punto, seguito da un nome, gli elementi
B) rappresentazione per elencazione: si scrive la lettera maiuscola con la quale si vuole indicare l'insieme, seguita da un uguale e una parentesi graffa, si scrivono separati da virgole i suoi elementi e si chiude la parentesi.
C) rappresentazione per caratteristica: si deve scrivere all'interno di una coppia di parentesi graffe "la proprietà" che caratterizza l'insieme.
1) Rappresenta in tutti i modi che conosci l'insieme A formato dalle lettere della parola bicchiere
Ricorda che un insieme è un raggruppamento di elementi definibili con precisione.
1) Indica quali dei seguenti raggruppamenti rappresentano un insieme in senso matematico:
a. l'insieme delle vocali presenti nel tuo cognome;
b. l'insieme dei numeri naturali minori di 5;
c. le più belle città d'Italia;
d. gli stati d'Europa;
e. i compagni più simpatici della tua classe.
ESERCIZI SULLA RAPPRESENTAZIONE DEGLI INSIEMI
Ricorda che un insieme si può rappresentare in tre modi:
A) con i diagrammi di Eulero-Venn, che sono formati da un ovale all'interno del quale si segnano con un punto, seguito da un nome, gli elementi
B) rappresentazione per elencazione: si scrive la lettera maiuscola con la quale si vuole indicare l'insieme, seguita da un uguale e una parentesi graffa, si scrivono separati da virgole i suoi elementi e si chiude la parentesi.
C) rappresentazione per caratteristica: si deve scrivere all'interno di una coppia di parentesi graffe "la proprietà" che caratterizza l'insieme.
1) Rappresenta in tutti i modi che conosci l'insieme A formato dalle lettere della parola bicchiere
giovedì 22 settembre 2016
Cinematica
Appunti di Cinematica
mercoledì 21 settembre 2016
martedì 20 settembre 2016
domenica 18 settembre 2016
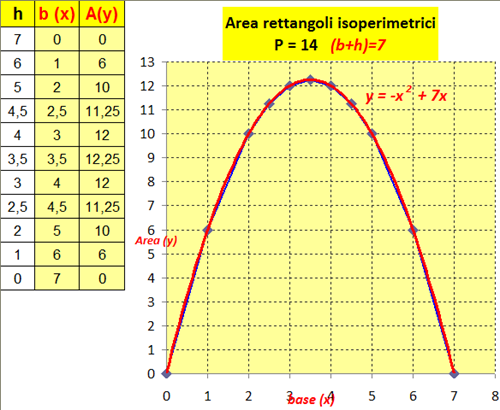
Rettangoli isoperimetrici
In III F
abbiamo lavorato ai rettangoli isoperimetrici con lo spago. Così, come mostra la gif (vedete ragazzi, trovata in rete, in un Omaggio a Emma Castelnuovo)

Potete osservare che sovrapposta alla curva di colore blu, ottenuta dalla tabella utilizzando solo valori interi della base e dell’altezza, è presente una curva rossa:
si tratta della linea di tendenza, la curva alla quale si avvicina il nostro grafico se “infittisco” la tabella con valori decimali della base (e dell’altezza).
Infatti, osservate sotto come la curva blu si avvicina sempre più alla curva rossa, quasi sovrapponendosi. Per sovrapporsi completamente potrei ancora infittire la tabella ... fra quali valori?
abbiamo lavorato ai rettangoli isoperimetrici con lo spago. Così, come mostra la gif (vedete ragazzi, trovata in rete, in un Omaggio a Emma Castelnuovo)
Dall’osservazione al calcolo, abbiamo visto che l’area del rettangolo varia mentre il perimetro rimane sempre lo stesso.
Abbiamo ragionato sui casi limite:
1. quando il rettangolo è "schiacciato" in orizzontale, la base b è uguale al semiperimetro, l'altezza h = 0 e quindi l'area A = bxh=0
2. quando il rettangolo è "schiacciato" in verticale, la base b = 0, l'altezza h = semiperimetro e
quindi l'area A = 0
Ora, ragazzi, dalla tabella di valori base-area devete costruire i grafici sul piano cartesiano. Verificherete che il grafico sarà la curva descritta da una palla lanciata in aria: la parabola.
Osservate bene i grafici d’esempio, con relative tabelle

Potete osservare che sovrapposta alla curva di colore blu, ottenuta dalla tabella utilizzando solo valori interi della base e dell’altezza, è presente una curva rossa:
si tratta della linea di tendenza, la curva alla quale si avvicina il nostro grafico se “infittisco” la tabella con valori decimali della base (e dell’altezza).
Infatti, osservate sotto come la curva blu si avvicina sempre più alla curva rossa, quasi sovrapponendosi. Per sovrapporsi completamente potrei ancora infittire la tabella ... fra quali valori?

sabato 17 settembre 2016
giovedì 15 settembre 2016
lunedì 18 aprile 2016
Problemi su Piano Cartesiano - III R
1 – Disegna sul piano cartesiano i punti A(-2;3) B(9;3) C(9;7) D(-2;7) e uniscili. Descrivi la figura ottenuta e calcola il suo perimetro, l’area e la diagonale.
2 - Rappresenta nel piano cartesiano i punti A(5;1) B (2;5) C(-1;1) D(2;-3) e congiungili nell’ordine dato:
a) classifica il quadrilatero ABCD giustificando la tua risposta
b) determina perimetro e area di tale quadrilatero
Nota bene: gli esercizi vanno fatti su foglio protocollo e consegnati Mercoledì 20 Aprile
Se avete problemi vi consiglio di ripassare da pag. 282 a 284 del libro di Algebra. In ogni caso potete scrivermi qui.
Problemi sul Teorema di Pitagora
- Calcola il perimetro e l’area di un triangolo rettangolo i cui cateti misurano rispettivamente 5 e 12 cm
- Calcola la misura del perimetro e dell’area di un trapezio rettangolo che ha le due basi di 38 cm e 74 cm e il lato obliquo di 45 cm. [104; 1512]
- Calcola l'area e il perimetro di un quadrato avente la diagonale di 28,28 cm.
- La diagonale di un campo quadrato misura 132,9 cm. Quanto si spende per recintarlo con una rete metallica che costa 4,25 euro al metro?
- In un rombo le diagonali misurano 16 cm e 12 cm. Calcola la misura delperimetro e dell’area del rombo. [40; 96]
Problemi sulle aree di poligoni
- Calcola l'area di un quadrato che ha il perimetro di 60 cm. [225]
- I terreni di gioco per la Lega Nazionale Professionisti italiana di calcio devono avere le dimensioni obbligatorie di m 105 x 68. E' tollerata, per il lato corto, la dimensione minima di m 65 nei soli casi di comprovate difficoltà tecniche dell'impianto. Calcola la differenza tra le due superfici e tra i perimetri dei due casi.
- In un parallelogramma la base misura 24 cm e l’area è di 360 cm2. Calcola l’altezza del parallelogramma. [15]
- Calcola l’altezza di un triangolo sapendo che la base misura 72 cm e che l’area misura 6084 cm2 [169]
Iscriviti a:
Commenti (Atom)





























